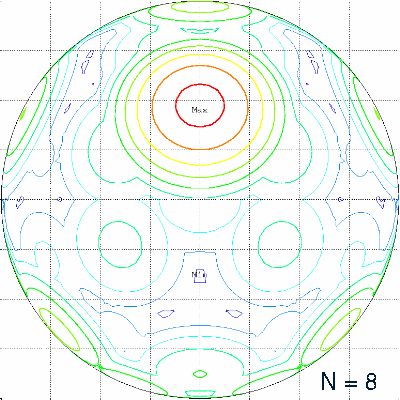
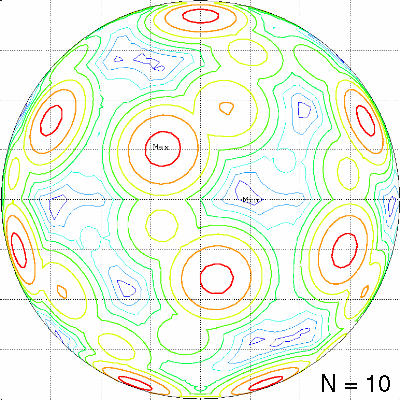
| Criterion | Value |
| Minimize difference: | (Imax - Imin) / 2 |
| Maximize minimum: | N/4 - Imin |
| Minimize maximum: | Imax - N/4 |
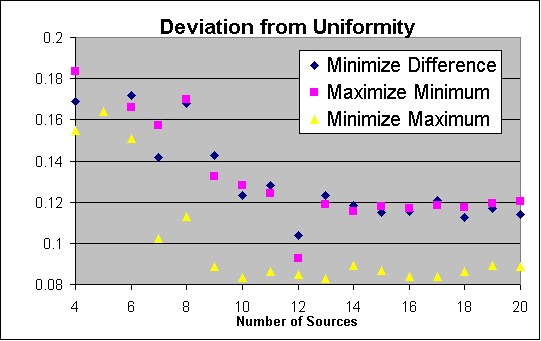
| Criterion | Value |
| Minimize difference: | (Imax - Imin) / 2 |
| Maximize minimum: | N/4 - Imin |
| Minimize maximum: | Imax - N/4 |

For N=5 only the "minimize maximum" results are shown, because the other two results would require an extension of the scale (0.51787/2=0.25893 for "minimize difference" and 1.25-0.93969=0.31031 for "maximize minimum").
The character of the optimal solutions is different, dependent on the applied criterion. A typical property of the "minimize maximum" configurations is the occurrence of at least 2N luminance maxima with a smooth behavior in the neighbourhood of the maxima. As the value of the minimum luminance has no influence on the objective function, there are often a few "dark holes" in the optimal luminance pattern, as can be seen in the lower half of the following picture: